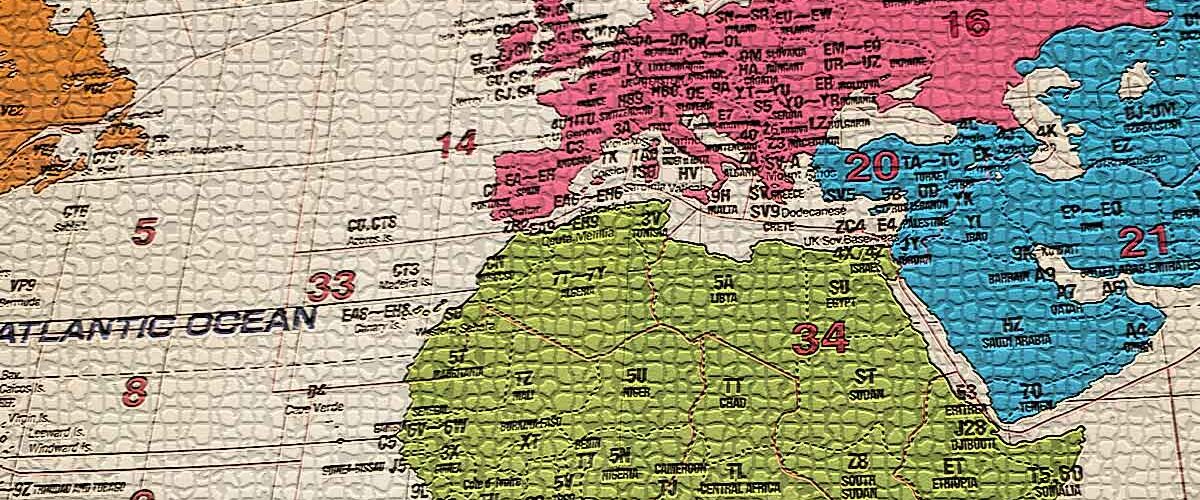
Пълен списък на радиолюбителските префикси Настоящият списък съдържа всички (или поне почти всички) префикси, които могат да се чуят в радиолюбителския ефир към 9 март 2024 година. Списъкът е събиран и поддържан години. Надявам се да е полезен на много колеги-радиолюбители. Наименованията са на английски език. По моя преценка не […]
Пълен списък на радиолюбителските кодове, съкращения и изрази Не претендирам да е абсолютен пълен, мога да претендирам само че е пълният списък, който аз съм чувал в дейността си като радиолюбител (последните 50 години от живота си). Код Значение Бележки . . (две точки) Бъди здрав! Всичко хубаво! Довиждане! Бай-бай! […]
Разширяване на обхвата на предаване Предистория Преди време един приятел и радиолюбител (не пиша кой е, защото не съм го питал дали може) сподели, че не може да излъчва на част от 60 м диапазон. Предполагаше, че трансивърът му Yaesu FTDX-10, тъй като е подготвен за Испания, отразява испанските регламенти. […]
Актуализация на фърмуера на FTDX-10 Това звучи страшно, но не е. Или не е поне докато не се случи някакъв фал – например да спре електрическия ток у вас точно в този момент. Но нека не бъдем черногледи… Ако всичко е изправно и спазваш процедурата, не би трябвало да се […]
Две напълно излишни настройки за FTDX-10 Но всеки иска първо тях да направи Нужно ли е да правим тези две напълно излишни настройки? Първата е персонализиран екран при включване. Кой не иска да си пероснализира новото радио, като го накара да показва неговото име или позивна? Едва ли има някой, […]
Последните ми радиовръзки Това е извадка от QRZ.com за радиовръзките, направени от мен (Тони, LZ3AI). Тези радиовръзки (QSOs) обикновено не са последните. Самата извадка е в реално време и показва последните, качени в QRZ.com, но не и последните направени и отразени в локалния дневник (logbook). Обикновено са или DX, или свързани […]
Може ли хакер да дешифрира съобщения на Telegram? Много хора нямат доверие в сигурността на комуникациите с Телеграм. Вероятно този текст и линковете в него ще бъдат достатъчно красноречиви. Вижте тази страница за най-новите подробности относно програмата за награди за грешки на Telegram. Всеки, който твърди, че съобщенията в Telegram могат да […]
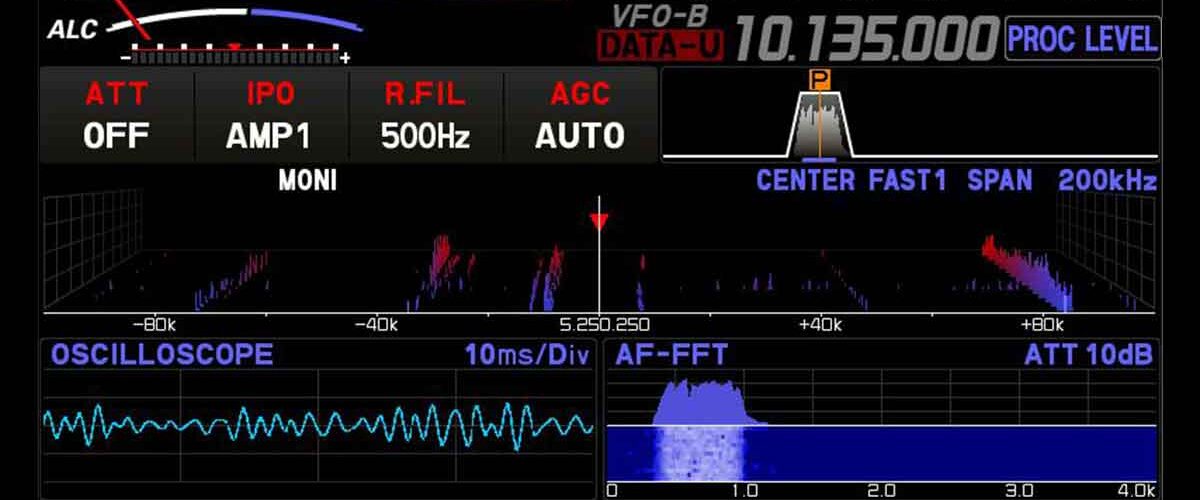
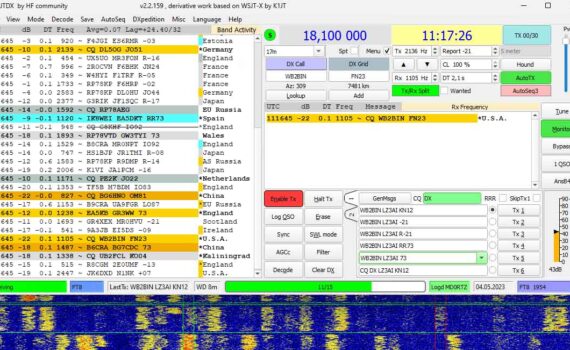
Ще споделя личния опит с Yaesu FTDX-10, FT8 и JTDX. Започвам от свързването на апаратурата. Стари радиолюбители ми казваха, че трябва да си направя или купя интерфейсна приставка, с която да свържа компютъра през аудио-вход/изход на трансивъра, защото сервизите били пълни с трансивъри за ремонт на изгорели USB-портове. Е, то […]
Контрол Съгласно “Техническите изисквания” и “Закона за електронните съобщения” (ЗЕС) контролът по осъществяването на радиолюбителската дейност в ефир се извършва от КРС, като установяването на нарушения и налагането на наказания се извършва по реда на ЗЕС. За осъществяване на контрола радиолюбителят е длъжен да оказва съдействие на оправомощените служители на […]